格林定理在學電磁場和熱傳導等各方面都有重要作用。格林定理是數學中的一條重要定理，它揭示了平面區域上的積分與邊界曲線上的積分之間的關系。簡單來說，格林定理可以表述為：對于一個封閉的平面區域D，如果在區域D上對一個函數f(x,y)進行積分，那么這個積分值等于區域D的邊界曲線L上對函數f(x,y)的線積分值。

格林定理

格林定理的科學解釋可以從微積分的基本定理出發。微積分的基本定理告訴我們，一個函數在一個區域上的積分可以通過將該函數表示為兩個偏導數的函數，并對該函數在區域邊界上的積分進行計算來得到。而格林定理則進一步推廣了這個結果，它允許我們將一個函數在封閉區域上的積分轉化為邊界曲線上的線積分。

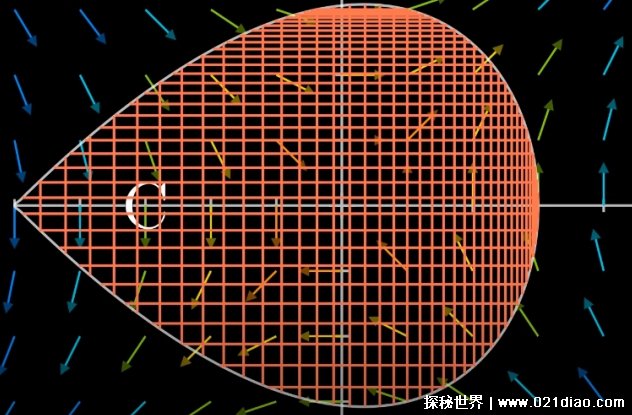
實際應用

在物理學中，電場和磁場可以用矢量場來表示。通過應用格林定理，我們可以更容易地計算出這些場在某個區域內的積分，從而得到該區域的電場強度或磁場強度。在電路分析中，電流和電壓可以看作是分布在一個電路上的標量場。通過應用格林定理，我們可以方便地計算出電路上的總電流或總電壓，從而對電路進行分析和設計。

廣泛使用

在解決熱傳導問題時，我們常常需要計算溫度場的分布。通過應用格林定理，可以方便地計算出溫度場在一個封閉區域內的積分，從而得到該區域的平均溫度或最高溫度等參數。在流體力學中，格林定理也被廣泛應用于流體流動的分析和計算，可以利用格林定理來計算流體在一個封閉區域內的速度場或壓力場等參數。